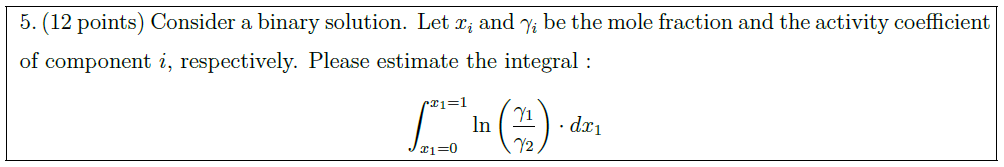Solution:
Consider a pure fluid whose equation of state is given by $\displaystyle \frac{PV}{RT} = 1 + \frac{B(T)}{V} + \frac{C(T)}{V^2}$, where $B$ and $C$ are the second and the third virial coefficients. Please answer the following questions.
\begin{parts}
\part [6] Determine the Helmholtz free energy $A$ at constant $T$.
\part [6] Suppose $C$ is a positive constant. Also assume that $B$ varies with $T$ according to $B = v_2 (1 – T_0/T)$, where $v_2$ is a positive constant and $T_0$ is the Boyle temperature at which $B$ vanishes. The objective here is to see how $A$ behaves as a function of the molar density $\rho \equiv 1/V$ when decreasing $T$ from $T \gg T_0$ to $T \ll T_0$. You expect to get a family of curves whose shapes vary with $T$. Sketch these curves in the $A$–$\rho$ plane.
\part [9] You might observe in (b) that $A$ can vary monotonically with $\rho$ for some range of $T$ and exhibit maximum/minimum for the other. In the latter case, what does it imply? What would happen to the fluid? Provide your physical explanations.
\part [12] There exists a critical temperature $T_c$ that separates the monotonic and non–monotonic free energy profiles. Determine $T_c$ in terms of $C$, $v_2$, and $T_0$. What is the corresponding molar density $\rho_c$? For $T > T_c$, what $\uline{\mbox{state}}$ would the fluid be situated at? Explain your answer physically.
\end{parts}