Solution:
\begin{parts}
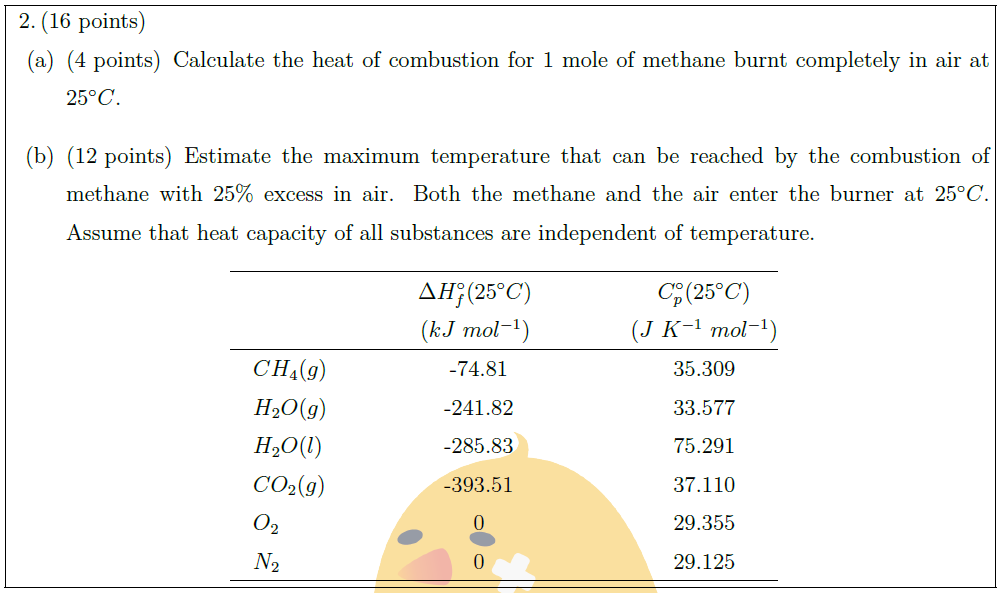
\part [4] Calculate the heat of combustion for 1 mole of methane burnt completely in air at $25^\circ C$.
\part [12] Estimate the maximum temperature that can be reached by the combustion of methane with $25 \%$ excess in air. Both the methane and the air enter the burner at $25^\circ C$. Assume that heat capacity of all substances are independent of temperature.
\end{parts}
\begin{center}
\begin{tabular}{@{}lcc@{}}
\hline
& \begin{tabular}{@{}c@{}} $\Delta H_f^{\circ} (25^\circ C)$\\
($kJ\ mol^{-1}$) \end{tabular} \quad \quad & \quad \quad \begin{tabular}{@{}c@{}} $C_p^{\circ} (25^\circ C)$\\
($J\ K^{-1}\ mol^{-1}$) \end{tabular}\\
\hline
\quad $CH_4 (g)$\quad \quad \quad \quad & -74.81\quad \quad & \quad \quad 35.309\\
\quad $H_2 O (g)$\quad \quad \quad \quad & -241.82\quad \quad & \quad \quad 33.577\\
\quad $H_2 O (l)$\quad \quad \quad \quad & -285.83\quad \quad & \quad \quad 75.291\\
\quad $CO_2 (g)$\quad \quad \quad \quad & -393.51\quad \quad & \quad \quad 37.110\\
\quad $O_2$\quad \quad \quad \quad & 0\quad \quad & \quad \quad 29.355\\
\quad $N_2$\quad \quad \quad \quad & 0\quad \quad & \quad \quad 29.125\\
\hline
\end{tabular}
\end{center}