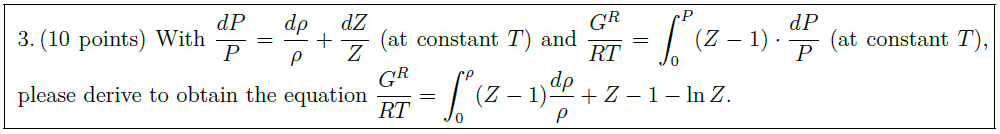Solution:
With $\displaystyle \frac{dP}{P} = \frac{d \rho}{\rho} + \frac{dZ}{Z}$ (at constant $T$) and $\displaystyle \frac{G^R}{RT} = \int_0^P (Z – 1) \cdot \frac{dP}{P}$ (at constant $T$), please derive to obtain the equation $\displaystyle \frac{G^R}{RT} = \int_{0}^{\rho} (Z – 1) \frac{d \rho}{\rho} + Z – 1 – \ln Z$.