Solution:
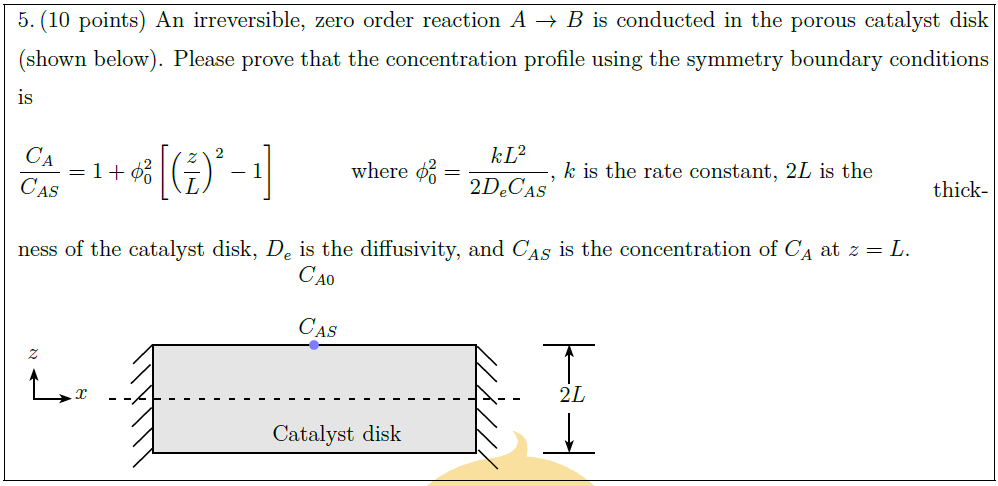
An irreversible, zero order reaction $A \to B$ is conducted in the porous catalyst disk (shown below). Please prove that the concentration profile using the symmetry boundary conditions is\\
\\
\begin{tabular}{@{}l@{}}
$\displaystyle \frac{C_A}{C_{AS}} = 1 + \phi_0^2 \left[ \left( \frac{z}{L} \right)^2 – 1 \right]$\hspace*{3em} where $\displaystyle \phi_0^2 = \frac{kL^2}{2 D_e C_{AS}}$, $k$ is the rate constant, $2L$ is the \\
\\
\end{tabular}
thickness of the catalyst disk, $D_e$ is the diffusivity, and $C_{AS}$ is the concentration of $C_A$ at $z = L$.